Numbering Your Genealogy: Basic Systems, Complex Families and International Kin

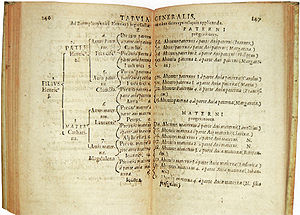
The first Ahnentafel, published by Michaël Eytzinger in Thesaurus principum hac aetate in Europa viventium Cologne: 1590, pp. 146-147, in which Eytzinger first illustrates his new functional theory of numeration of ancestors; this schema showing Henry III of France as n° 1, de cujus, with his ancestors in 5 generations.

Several genealogical numbering systems have been widely adopted for presenting family trees and pedigree charts in text format. Amid the well-nigh popular numbering systems are: Ahnentafel (Sosa-Stradonitz Method), and the Register, NGSQ, Henry, d'Aboville, Meurgey de Tupigny, and de Villiers/Pama Systems^{[ citation needed ]}.

Ascending numbering systems [edit]

Ahnentafel [edit]

Ahnentafel, besides known equally the Eytzinger Method, Sosa Method, and Sosa-Stradonitz Method, allows for the numbering of ancestors beginning with a descendant. This system allows ane to derive an ancestor's number without compiling the complete list, and allows ane to derive an ancestor's relationship based on their number. The number of a person's father is twice their own number, and the number of a person'south mother is twice their ain, plus one. For instance, if John Smith is 10, his father is 20, and his mother is 21.

In order to readily accept the generation stated for a certain person, the Ahnentafel numbering may be preceded by the generation. This method's usefulness becomes credible when practical further back in the generations: due east.1000. 08-146, is a male preceding the subject by 7 (viii-one) generations. This ancestor was the father of a adult female (146/two=73) (in the genealogical line of the subject area), who was the female parent of a man (73/two=36.v), further down the line the father of a homo (36/2=18), father of a woman (eighteen/two=9), mother of a man (nine/2=4.five), father of the subject'southward male parent (4/2=two). Hence, 08-146 is the subject's father'due south father's mother's father'south father's mother's male parent.

The atree or Binary Ahnentafel method is based on the aforementioned numbering of nodes, but beginning converts the numbers to binary notation and then converts each 0 to M (for Male) and each i to F (for Female person). The starting time graphic symbol of each code (shown as 10 in the table below) is M if the subject is male person and F if the subject field is female. For example 5 becomes 101 and so FMF (or MMF if the field of study is male). An advantage of this arrangement is easier understanding of the genealogical path.

The first 15 codes in each organization, identifying individuals in four generations, are as follows:

Human relationship	Without	With	Binary (atree)
	Generation
First Generation
Subject	1	1–1 or 01–001	X
Second Generation
Father	2	two–2 or 02-002	XM
Mother	3	two–iii or 02-003	XF
Third Generation
Father'south male parent	4	three–4 or 03-004	XMM
Father's female parent	5	3–v or 03-005	XMF
Mother's father	6	3–6 or 03-006	XFM
Female parent's mother	7	3–7 or 03-007	XFF
Fourth Generation
Father'due south father's father	8	four–8 or 04-008	XMMM
Father's father's mother	9	four–9 or 04-009	XMMF
Begetter'southward mother'south begetter	10	4–10 or 04-010	XMFM
Father's mother's mother	xi	iv–11 or 04-011	XMFF
Female parent's father's begetter	12	4–12 or 04-012	XFMM
Female parent'south father's mother	13	four–13 or 04-013	XFMF
Female parent's mother's begetter	fourteen	iv–14 or 04-014	XFFM
Mother's female parent's mother	15	4–xv or 04-015	XFFF

Surname methods [edit]

Genealogical writers sometimes cull to present ancestral lines past carrying back individuals with their spouses or unmarried families generation by generation. The siblings of the individual or individuals studied may or may not be named for each family unit. This method is most popular in simplified single surname studies, however, allied surnames of major family unit branches may be carried back besides. In general, numbers are assigned simply to the primary private studied in each generation.^[1]

Descending numbering systems [edit]

Register Arrangement [edit]

The Register System uses both common numerals (1, 2, 3, four) and Roman numerals (i, two, iii, iv). The organisation is organized by generation, i.e., generations are grouped separately.

The organisation was created in 1870 for use in the New England Historical and Genealogical Register published by the New England Historic Genealogical Society based in Boston, Massachusetts. Register Way, of which the numbering system is function, is one of two major styles used in the U.S. for compiling descending genealogies. (The other being the NGSQ System.)^[2]

          (–Generation One–)  1 Progenitor      2     i  Child           two  Child (no progeny)          iii  Child (no progeny)      iii    iv  Child        

          (–Generation Two–) 2 Child            i  Grandchild (no progeny)           ii  Grandchild (no progeny) three Child      4     i  Grandchild        

          (–Generation Three–) 4 Grandchild      5     i  Great-grandchild           ii  Great-grandchild (no progeny)      half-dozen   iii  Neat-grandchild      7    iv  Corking-grandchild        

NGSQ Organization [edit]

The NGSQ System gets its name from the National Genealogical Society Quarterly published by the National Genealogical Society headquartered in Falls Church, Virginia, which uses the method in its articles. It is sometimes chosen the "Record System" or the "Modified Register System" because it derives from the Register System. The nearly significant difference between the NGSQ and the Annals Systems is in the method of numbering for children who are not carried frontward into hereafter generations: The NGSQ System assigns a number to every child, whether or not that child is known to take progeny, and the Annals System does not. Other differences betwixt the two systems are by and large stylistic.^[one]

          (–Generation One–)  i Progenitor   +  2     i  Child      3    two  Kid (no progeny)      4   iii  Child (no progeny)   +  5    4  Kid        

          (–Generation Two–) 2 Child      6     i  Grandchild (no progeny)      vii    ii  Grandchild (no progeny) v Kid   +  viii     i  Grandchild        

          (–Generation Three–) eight Grandchild   +  ix     i  Great-grandchild     10    ii  Great-grandchild (no progeny)   + 11   iii  Great-grandchild   + 12    iv  Not bad-grandchild        

Henry System [edit]

The Henry System is a descending system created by Reginald Buchanan Henry for a genealogy of the families of the presidents of the United states that he wrote in 1935.^[3] It can be organized either by generation or not. The system begins with one. The oldest kid becomes 11, the adjacent child is 12, so on. The oldest kid of 11 is 111, the adjacent 112, and and so on. The system allows one to derive an ancestor's relationship based on their number. For example, 621 is the first child of 62, who is the 2d kid of 6, who is the 6th child of his parents.

In the Henry Organization, when there are more than than ix children, X is used for the 10th child, A is used for the 11th child, B is used for the 12th child, and then on. In the Modified Henry System, when at that place are more than than 9 children, numbers greater than nine are placed in parentheses.

          Henry          Modified Henry          1. Progenitor 		               1. Progenitor     11. Child		                  11. Kid        111. Grandchild		              111. Grandchild             1111. Great-grandchild                1111. Great-grandchild             1112. Great-grandchild                1112. Cracking-grandchild        112. Grandchild		              112. Grandchild    12. Kid		                  12. Child        121. Grandchild		              121. Grandchild             1211. Great-grandchild                1211. Bully-grandchild             1212. Not bad-grandchild                1212. Great-grandchild        122. Grandchild		              122. Grandchild             1221. Great-grandchild                1221. Bang-up-grandchild        123. Grandchild		              123. Grandchild        124. Grandchild		              124. Grandchild        125. Grandchild		              125. Grandchild        126. Grandchild		              126. Grandchild        127. Grandchild		              127. Grandchild        128. Grandchild		              128. Grandchild        129. Grandchild		              129. Grandchild        12X. Grandchild		              12(10). Grandchild        

d'Aboville System [edit]

The d'Aboville System is a descending numbering method developed past Jacques d'Aboville in 1940 that is very similar to the Henry Organization, widely used in France.^[4] It can be organized either past generation or not. Information technology differs from the Henry System in that periods are used to separate the generations and no changes in numbering are needed for families with more than than nine children.^[5] For example:

i Progenitor   one.1 Child       1.1.one Grandchild             1.1.1.one Great-grandchild             1.1.ane.ii Bully-grandchild       1.1.2 Grandchild   one.ii Child       1.2.ane Grandchild             1.2.1.i Great-grandchild             1.ii.1.2 Slap-up-grandchild       1.two.ii Grandchild             1.two.two.ane Great-grandchild       1.two.iii Grandchild       1.2.4 Grandchild       i.2.5 Grandchild       one.2.half-dozen Grandchild       one.2.7 Grandchild       ane.2.8 Grandchild       1.two.9 Grandchild       i.2.ten Grandchild        

The Huntington Family Association used this numbering system in their family memoir published in 1915, 25 years before Jacques d'Aboville is credited with inventing it.^{[ citation needed ]} It may very well be true the Huntington family unit invented this numbering system.^{[ commendation needed ]}

Meurgey de Tupigny System [edit]

The Meurgey de Tupigny Organization is a simple numbering method used for single surname studies and hereditary nobility line studies adult by Jacques Meurgey de Tupigny [Wikidata] of the National Athenaeum of France, published in 1953.^[6]

Each generation is identified past a Roman numeral (I, II, III, ...), and each child and cousin in the aforementioned generation conveying the same surname is identified by an Arabic numeral.^[seven] The numbering organisation normally appears on or in conjunction with a pedigree nautical chart. Example:

I Progenitor   II-1 Child        III-1 Grandchild              Iv-1  Great-grandchild              IV-2  Nifty-grandchild         III-2 Grandchild        III-three Grandchild        Iii-four Grandchild   2-2 Child        III-5 Grandchild              Four-3  Bang-up-grandchild              Four-4  Nifty-grandchild               Four-5  Smashing-grandchild        III-vi Grandchild        

de Villiers/Pama Organisation [edit]

The de Villiers/Pama Organisation gives letters to generations, and and so numbers children in birth order. For example:

a Progenitor   b1 Child      c1 Grandchild         d1 Swell-grandchild         d2 Great-grandchild      c2 Grandchild      c3 Grandchild   b2 Child      c1 Grandchild         d1 Cracking-grandchild         d2 Great-grandchild         d3 Great-grandchild      c2 Grandchild      c3 Grandchild        

In this system, b2.c3 is the tertiary child of the second kid,^[eight] and is one of the progenitor'southward grandchildren.

The de Villiers/Pama system is the standard for genealogical works in South Africa. It was developed in the 19th century by Christoffel Coetzee de Villiers and used in his three volume Geslachtregister der Oude Kaapsche Familien (Genealogies of Quondam Cape Families). The organisation was refined by Dr. Cornelis (Cor) Pama, ane of the founding members of the Genealogical Gild of Southward Africa.^[ix]

See besides [edit]

• Ancestral File Number
• Ahnentafel
• Cousin chart (Tabular array of consanguinity)
• Family tree
• Family unit tree mapping
• GEDCOM
• Genogram
• Kinship terminology
• Pedigree chart
• Pedigree plummet

References [edit]

1. ^ ^{a b} Curran, Joan Ferris. Numbering Your Genealogy: Sound and Simple Systems. Arlington, Virginia: National Genealogical Guild, 1992.
2. ^ Curran, Joan Ferris, Madilyn Coen Crane, and John H. Wray.Numbering Your Genealogy: Bones Systems, Complex Families, and International Kin. Arlington, Virginia: National Genealogical Society, 1999.
3. ^ Henry, Reginald Buchanan. Genealogies of the Families of the Presidents. Rutland, Vermont: The Tuttle Company, 1935.
4. ^ Généalogie-Standard: Les systèmes de numérotation (Numbering Systems)
5. ^ Encyclopedia of Genealogy: d'Aboville Numbers
6. ^ Guide des recherches généalogiques aux Archives Nationales. Paris, 1953 (Bn : eight° L43 119 [1])
7. ^ "Standard GenWeb: La numérotation Meurgey de Tupigny". Archived from the original on 2008-06-23. Retrieved 2008-07-04 .
8. ^ Numbering Systems In Genealogy - de Villiers/Pama by Richard A. Pence
9. ^ Genealogical Guild of South Africa

Notes

• Nigh.com: Numbering Your Family Tree
• Numbering Systems in Genealogy by Richard A. Pence

External links [edit]

• Encyclopedia of Genealogy-Numbering Systems
• Numbering Systems in Genealogy

crabtreeclinking.blogspot.com

Source: https://en.wikipedia.org/wiki/Genealogical_numbering_systems

Share this post